Tìm hiểu thuật toán Counting Sort

Ý tưởng

Input: Đầu vào sẽ là n số nguyên trong khoảng [0,k], trong đó k là số nguyên, phạm vị giá trị của n và k = O(n)

Ý tưởng: Với mỗi phần tử x của dãy đầu vào ta xác định hạng (rank) của nó như là số lượng phần tử nhỏ hơn x. Một khi ta đã biết hạng r của x, ta có thể xếp nó vào vị trí r+1

Ví dụ: Nếu có 6 phần tử nhỏ hơn 17, ta có thể xếp 17 vào vị trí thứ 7.

Lặp: Khi có 1 loại phần tử có cùng giá trị, ta sẽ xếp chúng theo thứ tự xuất hiện trong dãy ban đầu để có được tính ổn định nhất của sắp xếp

Cài đặt

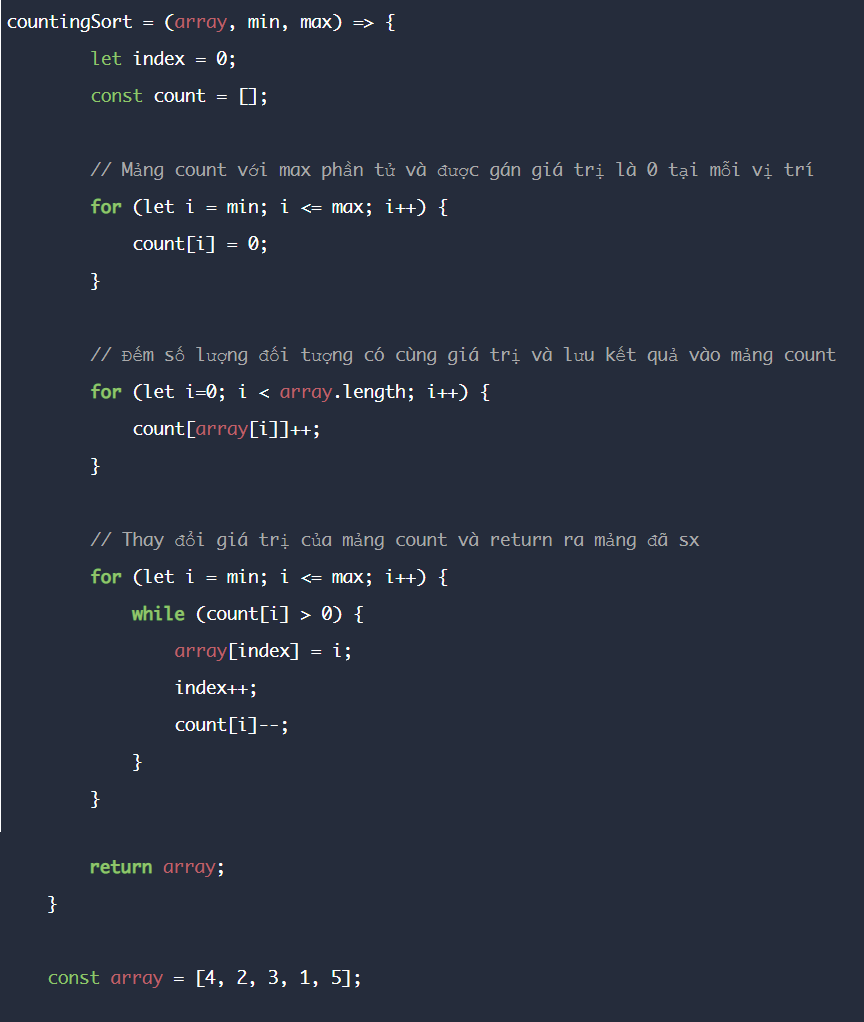
Ở đây tui sẽ dùng javascript để thực hiện ví dụ nhé🙂

Ở đây tui sẽ dùng C++ để thực hiện ví dụ nhé🙂

Sourcecode: Github

Độ phức tạp của thuật toán

• Counting Sort một thuật toán tuyến tính với độ phức tạp là O(n+k).
• Do k = O(n) nên thời gian của thuật toán là O(n) => thuật toán tốt nhất.
• Trường hợp k = n*n => Thuật toán làm việc rất tồi.
• Counting Sort không có tính tại chỗ.

Như vậy tui đã giới thiệu sơ qua về thuật toán Counting Sort và cách cài đặt nó trong js, C++.

Thanks for reading💖

Tài liệu tham khảo: giáo trình cấu trúc dữ liệu vào giải thuật – ĐHBKHN